Самарский Государственный Аэрокосмический Университет

Домашнее задание по физике №3

Выполнил студент 522 группы: Иванов А.

Проверил: Филонин Олег Васильевич

Самара 2001 г.

Условие задачи:

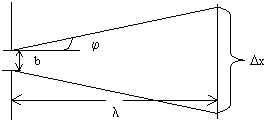
Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины b=1,0 мкм. Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние l=50 см, ширина центрального дифракционного максимума Dx=0,36 мм.

Решение:

Длина волны Де-бройля

Этой длине волны соответствует положение главного максимума, полученного от щели b.

l=b×sinj (т.к. Dx>>b, то (Dx–b)»Dx)

j®0

(5) в (4)

(6) в (2)

Условие задачи:

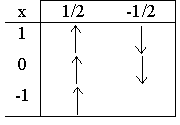
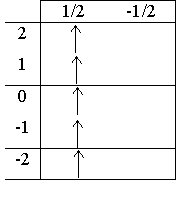
Выписать спектральные обозначения термов атома водорода, электрон которого находится в состоянии с главным числом n=3.

Решение:

По правилу Хунда

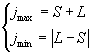
1) Пусть L=0

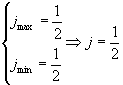
Обозначение :

2) Пусть L=1

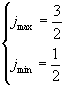
Обозначение :

3) Пусть L=2

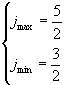
Обозначение :

Ответ:

Условие задачи:

Электронный пучок ускоряется в электронно-лучевой трубке разностью потенциалов U=0,5 кВ. Принимая, что неопределённость импульса равна 0,1% от его числового значения, определить неопределённость координаты электрона. Является ли в данных условиях электроны квантовой или классической частицей?

Решение:

Согласно соотношению неопределённостей ,

,

где -неопределённость координаты электрона;

-неопределённость его импульса.

Кинетическая энергия электрона, прошедшего ускоряющую разность потенциалов U:

,

импульс электрона:

Неопределённость импульса , т.е.

Неопределённость координаты электрона :

Ответ: x = 53,5 нм

Условие задачи:

Найти возможные мультиплетности c термов типа:

а) ^cD₂

б) ^cF₁

Решение:

a) ^cD₂

D Þ L=2

J=

шаг изменения n=1 S=0; 1; 2; 3; 4

мультиплетность

б) F

J=

шаг изменения n=1 S=2; 3; 4

мультиплетность

Ответ:

а)

б)

Условие задачи:

Частицы c массой m и энергией E движутся слева на потенциальный барьер. Найти :

а) коэффициент отражения R этого барьера при E>U₀;

б) эффективную глубину проникновения частиц в область x>0 при E<U₀, т.е. расстояние от границы барьера до точки, где плотность вероятности нахождения частиц уменьшится в e раз.

Решение:

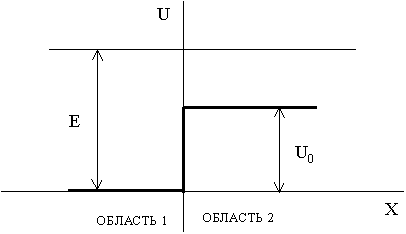
а) Запишем уравнение Шрёдингера для 1-ой и 2-ой области .

Для 1-ой области :

Для 2-ой области :

Пусть , ;

Получаем решения:

из (1) ,

из (2) .

Коэффициент прозрачности :

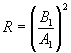
Т.к. в области x>0 имеется только проходящяя волна, то B₂=0.

Испльзуя и получим систему :

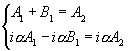
Пусть , , ; тогда

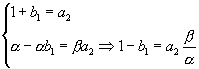
Откуда , тогда .

Получим коэффициент отражения :

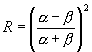
После подстановки получим окончательное выражение для коэффициента отражения:

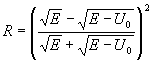
б) В случае E<U решение уравнения Шрёдингера для 2-ой области будет иметь вид :

,

где .

Т.к. в области x>0 при E<U волна распространяется в противоположном направлении, то A=0

Плотность вероятности нахождения частицы под барьером :

Из условия что P уменьшилась в e раз :

Получим ;

Проверим размерность:

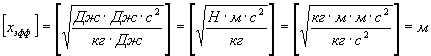
Ответ:

а) 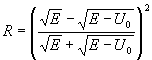б)

Условие задачи:

Вычислить дебройлевские длины волн электрона, протона и атома урана, имеющих одинаковую кинетическую энергию 100 эВ.

Решение:

.(1).

Значение кинетической энергии: .(2).

Подставляя (2) в (1), получаем: (3).

Проверим размерность:

Численно имеем: значит:

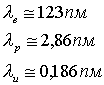
Ответ:123;2,86;0,186 пм.

Условие задачи:

Нейтрон с кинетической энергией T=25эВ налетает на покоящийся дейтрон. Найти дебройлевские длины волн обеих частиц в системе их центра инерции.

Решение:

Радиус-вектор центра инерции системы равен: ;

Продифференцируем последнее равенство и получим скорость центра инерции:

, где -скорость 1-ой частицы относительно центра инерции.

Получаем: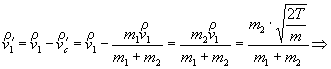

;

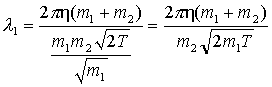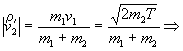
Проверим размерность:

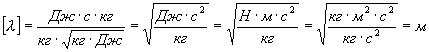
Ответ:

Условие задачи:

Частица массой m может двигаться вдоль оси X. Движение ограниченно непроницаемыми стенками x=0 и x=l .

Найти вероятность нахождения частицы в промежутке

при n=2.

Решение:

Вероятность нахождения частица в интервале :

P=

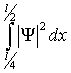
В данном случае потенциальная энергия U будет иметь вид :

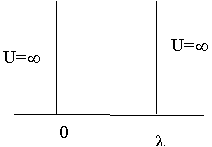
Частица может двигаться только вдоль оси X . Потенциальная энергия при равна нулю , а при и равна бесконечности .

Уравнение Шрёдингера в одномерном случае запишется в виде :

Так как вероятность нахождения частицы вне ямы равна нулю, то за пределами ямы .

Из условия непрерывности получаем : . В области , где уравнение Шрёдингера будет иметь вид :

, т.к. U=0 .

Пусть

Тогда

Решение этого уравнения имеет вид :

Для удовлетворения условий непрерывности выберем и :

Найдём собственные функции

Найдём коэффициент используя условие нормировки :

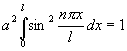
Таким образом для данного состояния n=2 :

P=

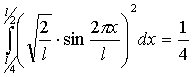
Ответ: P=

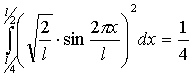
Условие задачи:

Определить, какую ускоряющую разность потенциалов должен пройти протон, чтобы длина волны де Бройля для него была 1 нм.

Решение:

Длина волны де Бройля: , импульс:

Получаем: , откуда

После подстановки числовых данных получим U=0,821 мВ

Ответ: U=0,821 мВ

Условие задачи:

Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, локализованного в области размером .

Решение:

соотношение неопределенностей:.

Т.к. атом локаоизован в области, то (1)

;(2) Из (1) и (2) следует, что

Проверка размерности:

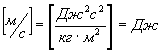
Ответ:

Условие задачи:

Сколько элементов содержится в ряду между теми, у которых длины волн -линий равны 250 и 179 пм?

Решение:

Найдем номера этих элементов, используя закон Мозли: .

Подставляя числа, получаем номера 23 и 27. А между этими числами расположены 3 числа. Значит между элементами, у которых длины волн -линий равны 250 и 179 пм, расположено еще 3 элемента.

Ответ: 3 элемента.

Условие задачи:

Найти возможные значения полных механических моментов атомов, находящихся в состояниях ⁴P и ⁵D.

Решение:

Для состояния ⁴P: мультиплетность равна 4; при Р получаем,
что L=1.

L=1 c=2×S+1=4 Þ S=3/2

J₁=1/2 Þ

J₂=3/2 Þ

J₃=5/2 Þ

Для состояния ⁵D : мультиплетность равна 5; при D получаем,
что L=2

L=2 c=2×S+1=5 Þ S=2

J₁=0 Þ

J₂=1 Þ

J₃=2 Þ

J₄=3 Þ

J₅=4 Þ

Условие задачи:

Узкий пучок моноэнергетических электронов падает под углом скольжения на естественную грань монокристалла алюминия. Расстояние между соседними кристаллическими плоскостями , параллельными этой грани монокристалла , При некотором ускоряющем напряжении U_o наблюдали максимум зеркального отражения. Найти U_o, если известно,что следующий максимум зеркального отражения возникал при увеличении ускоряющего напряжения враза.

Решение:

,где и -дебройлевские волны

составим систему уравнений :

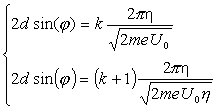
Þ 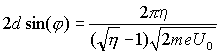Þ

Þ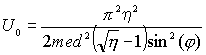

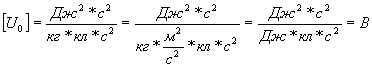
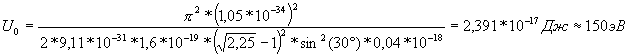
Ответ: 150Эв

Условие задачи:

Воспользовавшись правилами Хунда , найти число электронов в единственной незаполненной подоболочке атома , основной терм которого:

а)

б)

в)

Решение:

а) Þ Мультиплетность

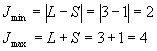
В данном случае

Число электронов = 2

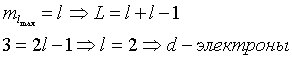
б) Þ Мультиплетность

5p электронов

в) Þ

Мультиплетность

5d электронов

Условие задачи:

Возбуждённый атом имеет электронную конфигурацию и находится при этом в состоянии с максимально возможным полным механическим моментом. Найти магнитный момент атома в этом состоянии .

Решение:

Магнитный момент

Механический момент - максимальный

Ответ:

Условие задачи:

Получить выражение для дебройлевской длины волны l релятивистской частицы, движущейся с кинетической энергией T. При каких значениях T ошибка в определении l по нерялитивистской формуле не превышает 1% для электрона и протона?

Решение:

Длина волны Дебройля

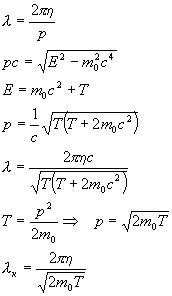
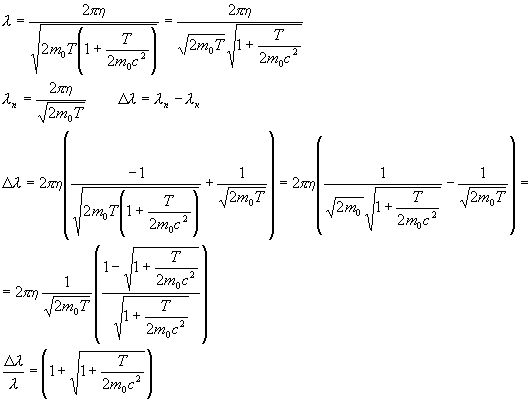
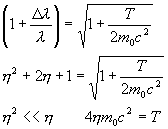
Точность соблюдается при

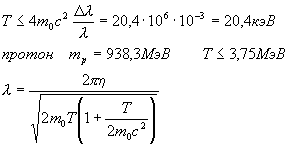
Условие задачи:

Найти дебройлевскую длину волны релятивистских электронов, подлетающих к антикатоду рентгеновской трубки ,если длина волны коротковолновой границы сплошного рентгеновского спектра

Решение:

-граничная длина волны (*)

-дебройлевская волна .Для релятивистских частиц импульс

энергия

,из(*)

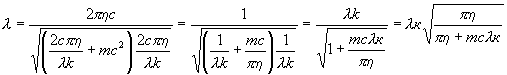
проверим размерность полученной величины:

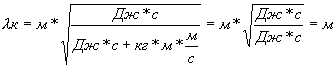
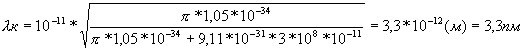
Ответ: 3,3 пм

Условие задачи:

Частица массой m находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найти возможные значения энергии частицы, если стороны ямы равны l₁ и l₂.

Решение:

В данном случае уравнение Шрёдингера примет вид:

, где

Внутри ямы решение уравнение Шрёдингера примет вид:

Возможные значения

и найдём из условия обращения Y в нуль на противоположных сторонах ямы:

Подстановка волновой функции в уравнение Шрёдингера приводит к соотношению , откуда

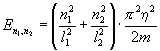
Проверим размерность:

Ответ: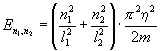

Условие задачи:

Показать, что для частицы, неопределенность местоположения которой , где - ее дебройлевская длина волны, неопределенность скорости равна по порядку величины самой скости частицы.

Решение:

Дебройлевская длина волны ,

Из соотношение неопределенносте получаем: .

Т.к. то .

Мы получили, что неопределенность скорости равна по порядку самой скорости частицы .

Условие задачи:

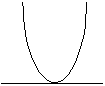
Волновая функция частицы массой m для основного состояния в одномерном потенциальном поле имеет вид , где А - нормировочный коэффициент, - положительная постоянная. Найти с помощью уравнения Шрёдингера постоянную a и энергию E частица в этом состоянии.

Решение:

Уравнение Шрёдингера :

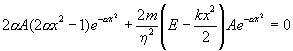
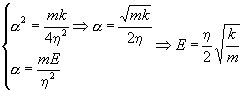
Ответ:

Условие задачи:

Найти частное решение одномерного временного уравнения Шредингера для свободно движущейся частицы массы m.

Решение:

Одномерное временное уравнение Шредингера имеет вид:

.

Решение будем искать в виде (*).

Подставив это решение в исходное уравнение, продифференцировав и разделив переменные получим:

.

Из этого уравнения получаем 2 уравнения:

Решая (1), получаем: , где ;(3).

Из (2) : .(4).

Подставим (3),(4) в (*), получим:

Ответ:

Условие задачи:

Найти возможные значения энергии частицы массы m, находящейся в сферически-симметричной потенциальной яме U(r)=0, при r<r₀ и U(r)=¥ при r=r₀, для случая, когда движение частицы описывается волновой функцией y(r), зависящей только от r.

Решение:

Уравнение Шрёдингера в сферических координатах

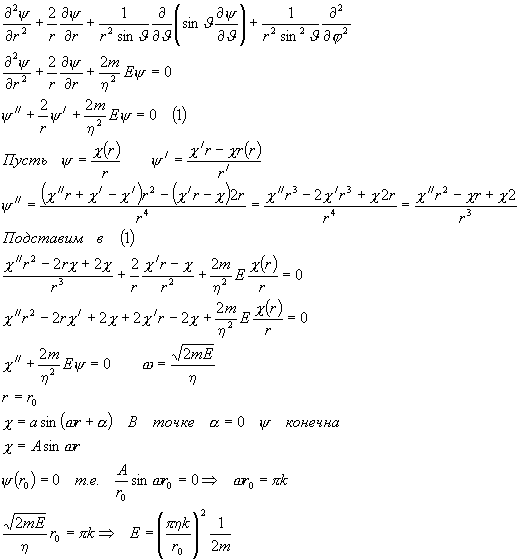
Условие задачи:

Оценить с помощью соотношения неопределенностей неопределенность скорости электрона в атоме водорода, полагая размер атома l=0,10 нм.

Решение:

Соотношение неопределенности: ;

но .

Неопределенность в координате электрона не может превышать размера атома, а максимальное значение .

Значит неопределенность скорости ,

Размерность:

Ответ: